The Partial Derivative of Okamoto’s Functions with Respect to the Parameter
What follows is a companion page to our paper “The Partial Derivative of Okamoto’s Function with respect to the parameter”. Here you will find an online version of the corresponding in-person talk given at the 13th AIMS Conference on Dynamical Systems, Differential Equations, and Applications, along with animations of relevant fractal surfaces and graphs.
Paper DOI: 10.14321/realanalexch.48.1.1638769133
Lebesgue’s Singular Function
Each (possibly unfair) coin (D2) determines a probability measure dependent on its weight as a value a in (0,1) induced by setting the probability of heads, (H), to a and the probability of tails, (T), to (1-a). Lebesgue’s Singular function gives the cdf of these probability distributions, and the change in the probability distribution can be studied by analyzing local properties of the surface.
Just below, one can see the surface derived from Lebesgue’s Singular function along with an animated graph showing the different cross sections of the surface for different a values.
*Below a values close to 0 are in green and a values close to 1 are in red, the cross-section animation obeys this convention as well.
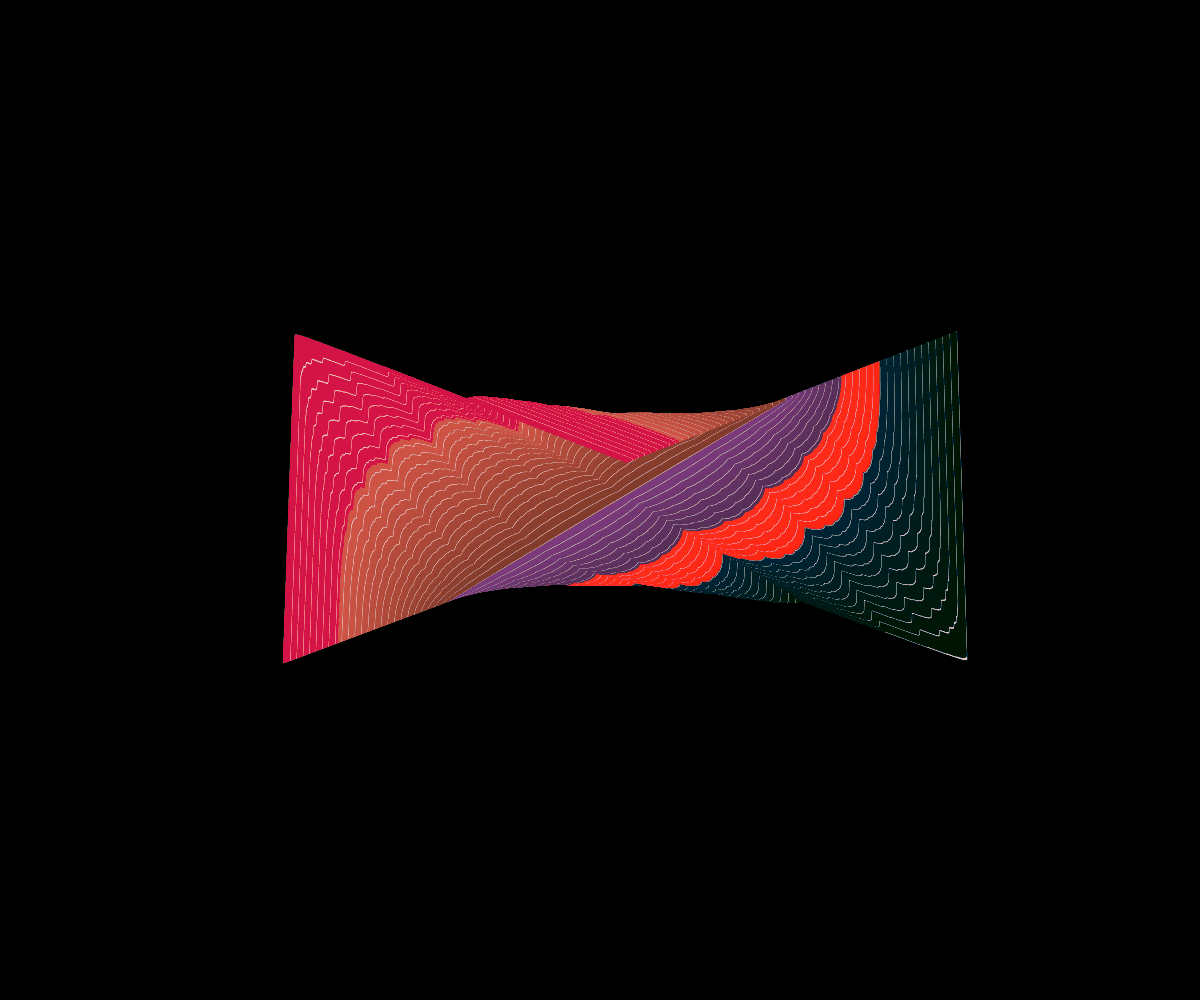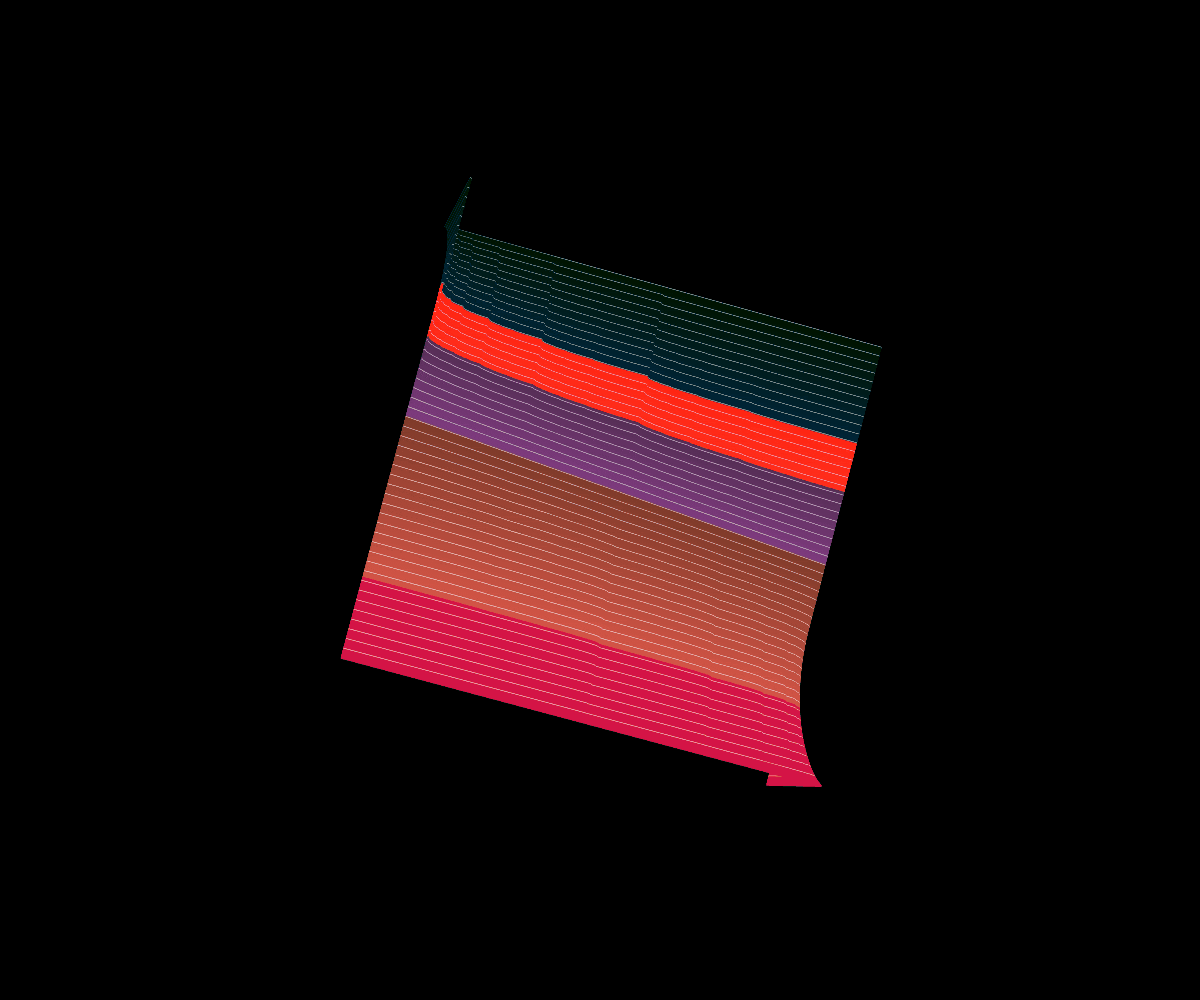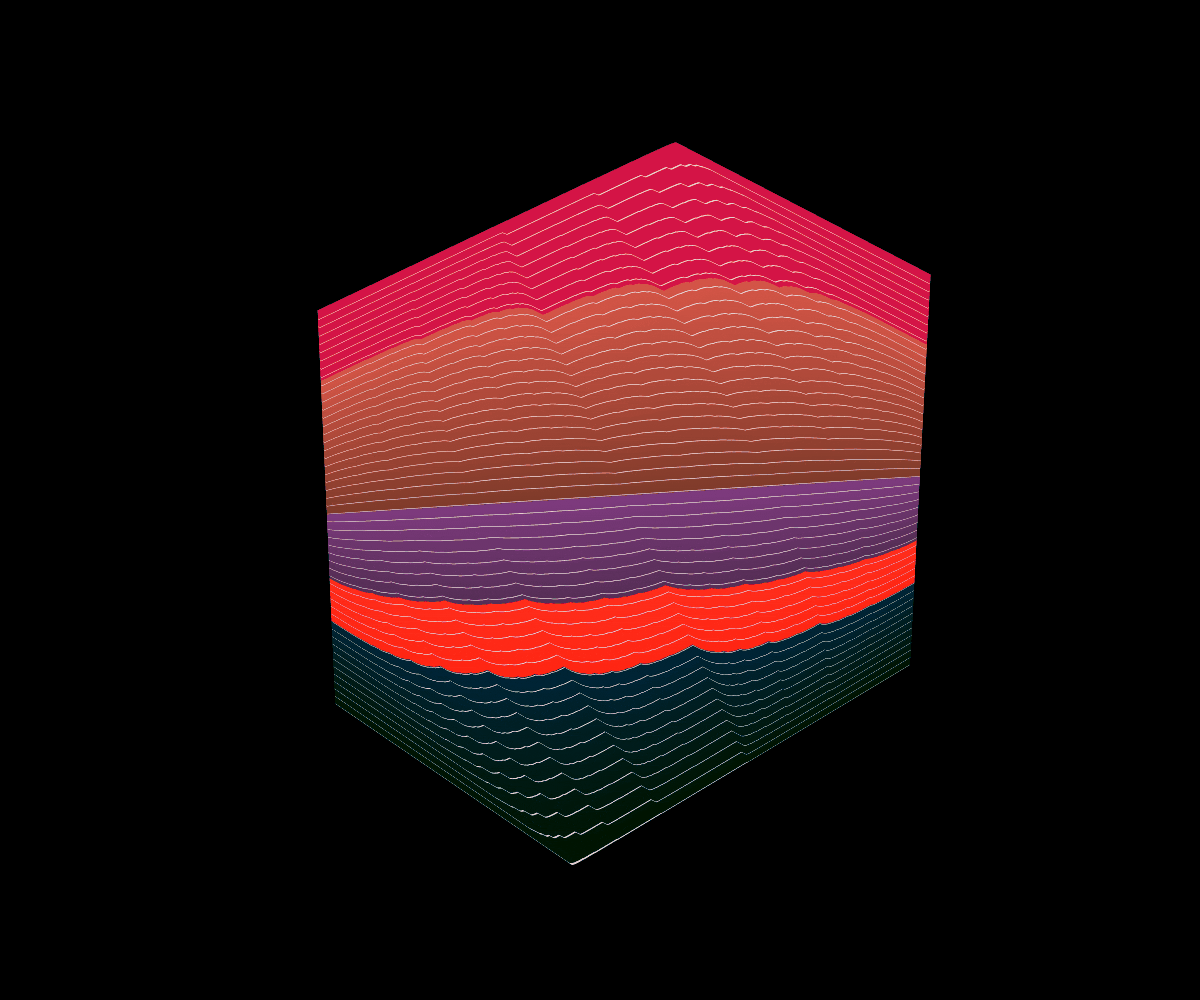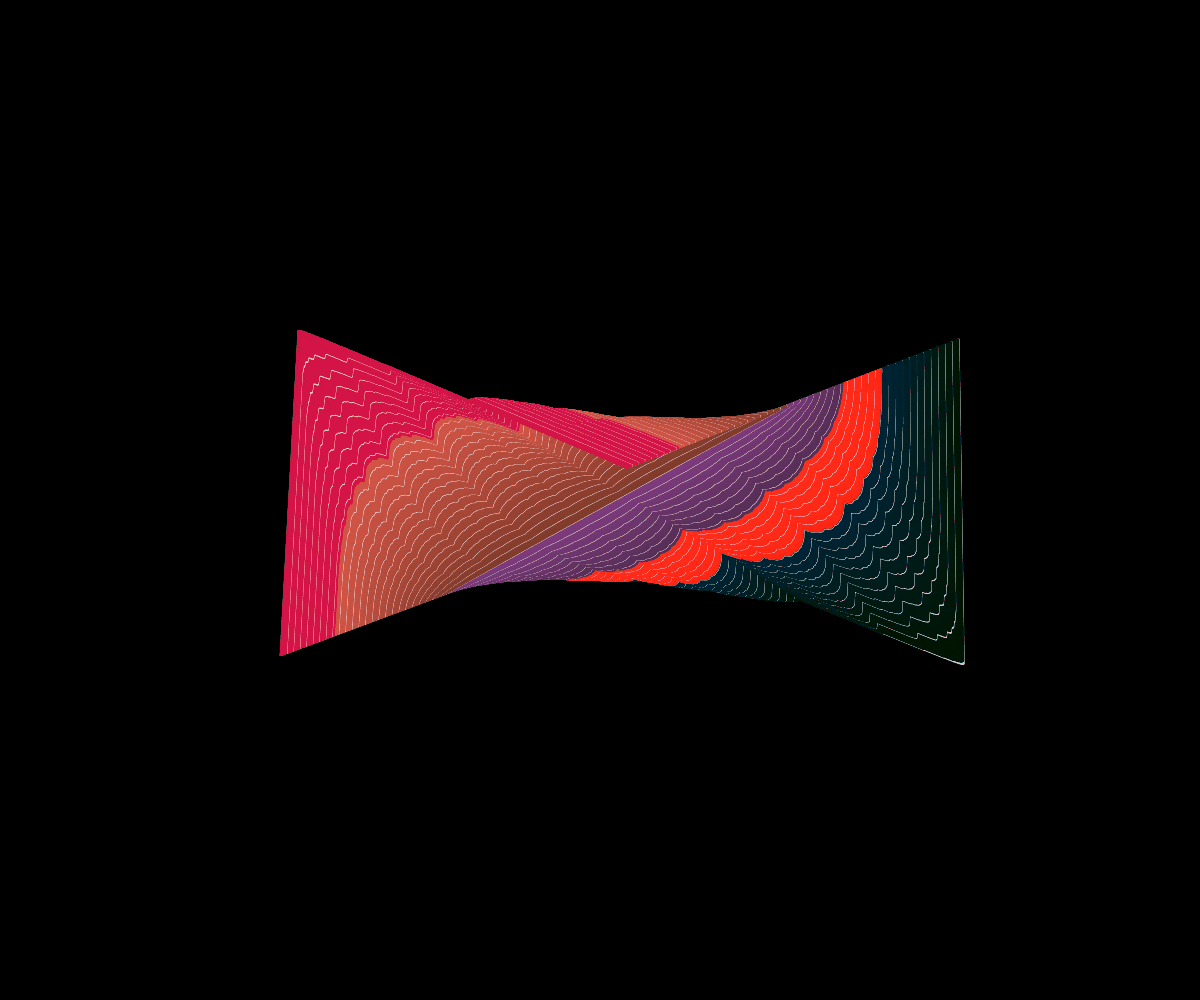
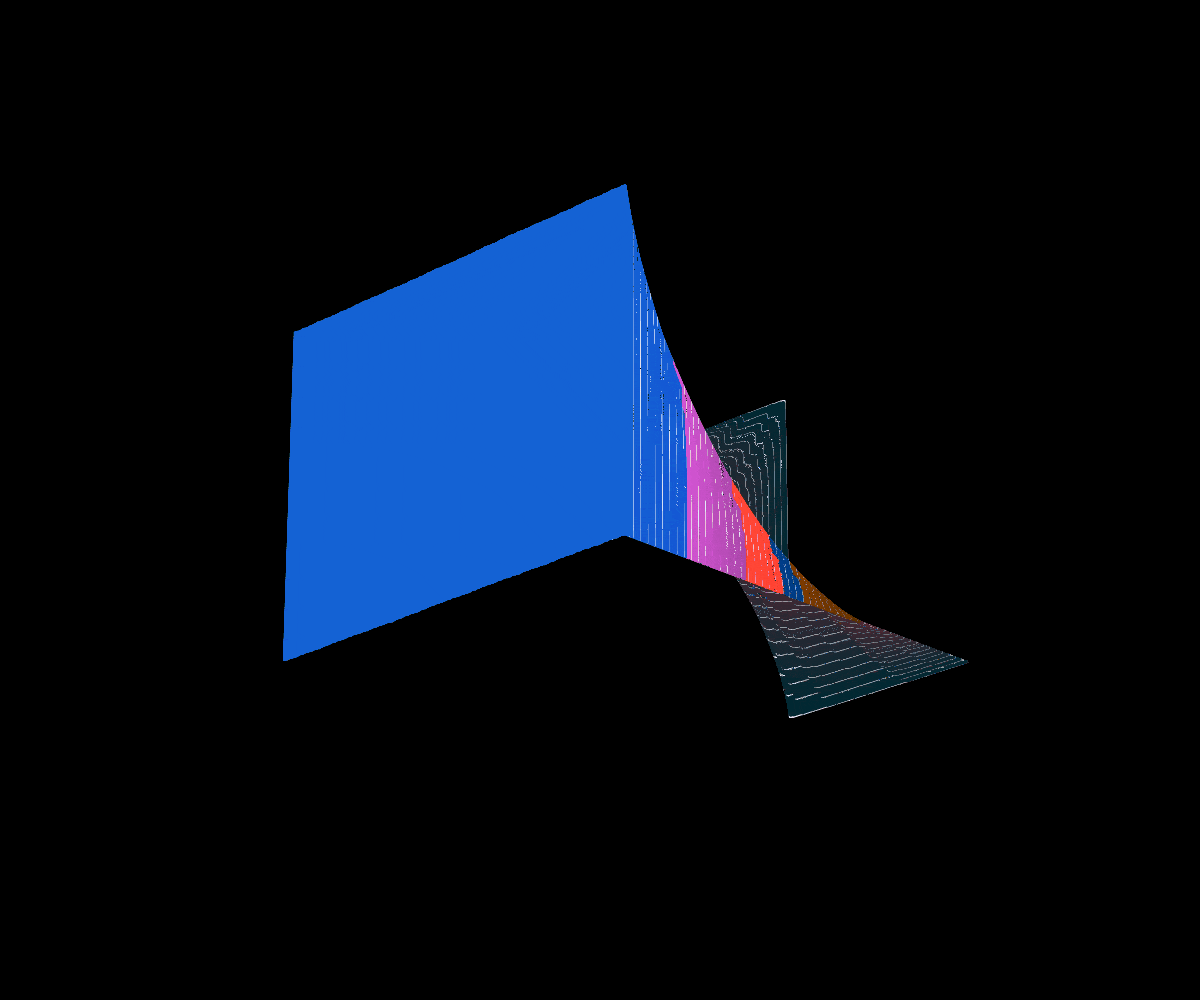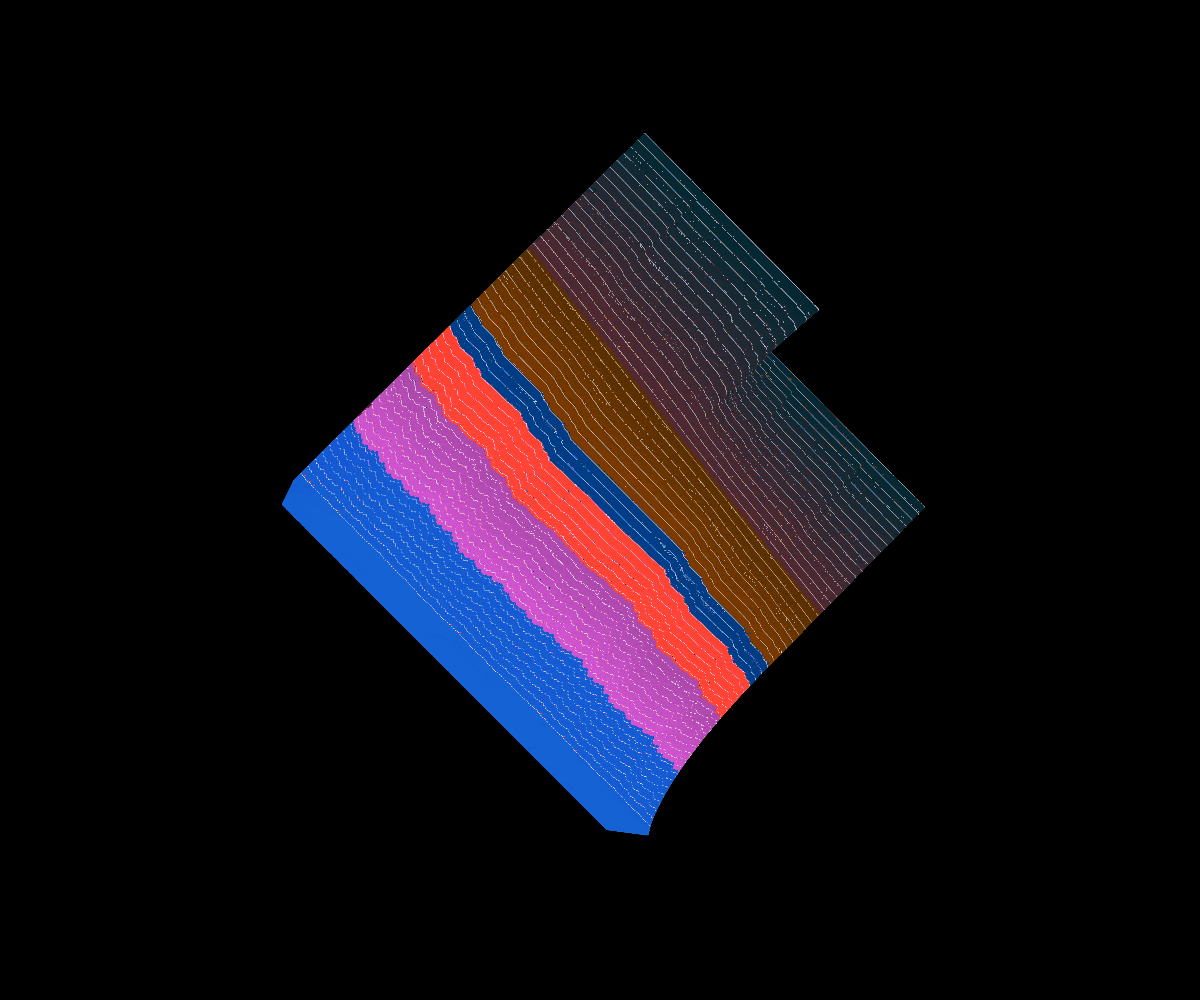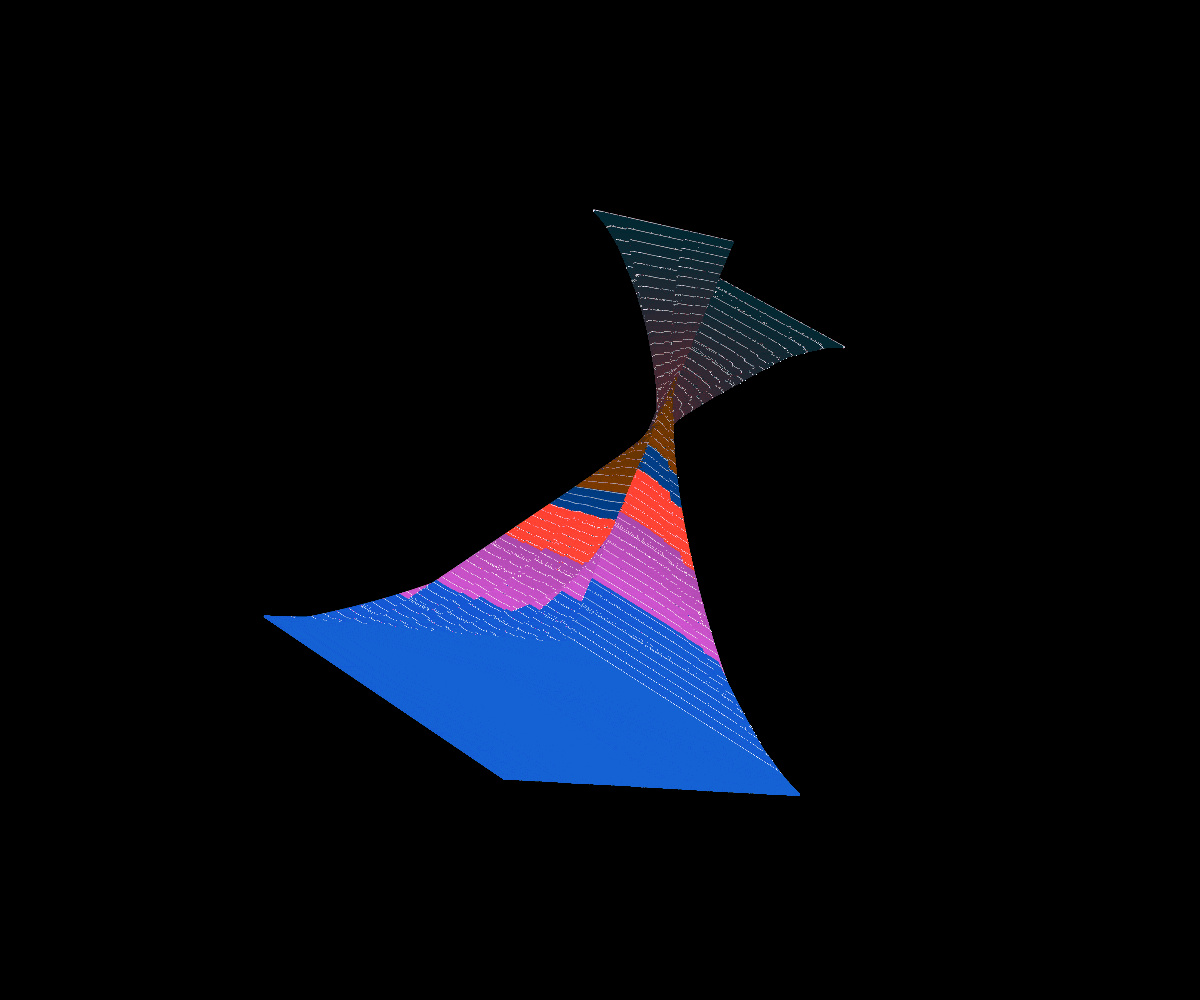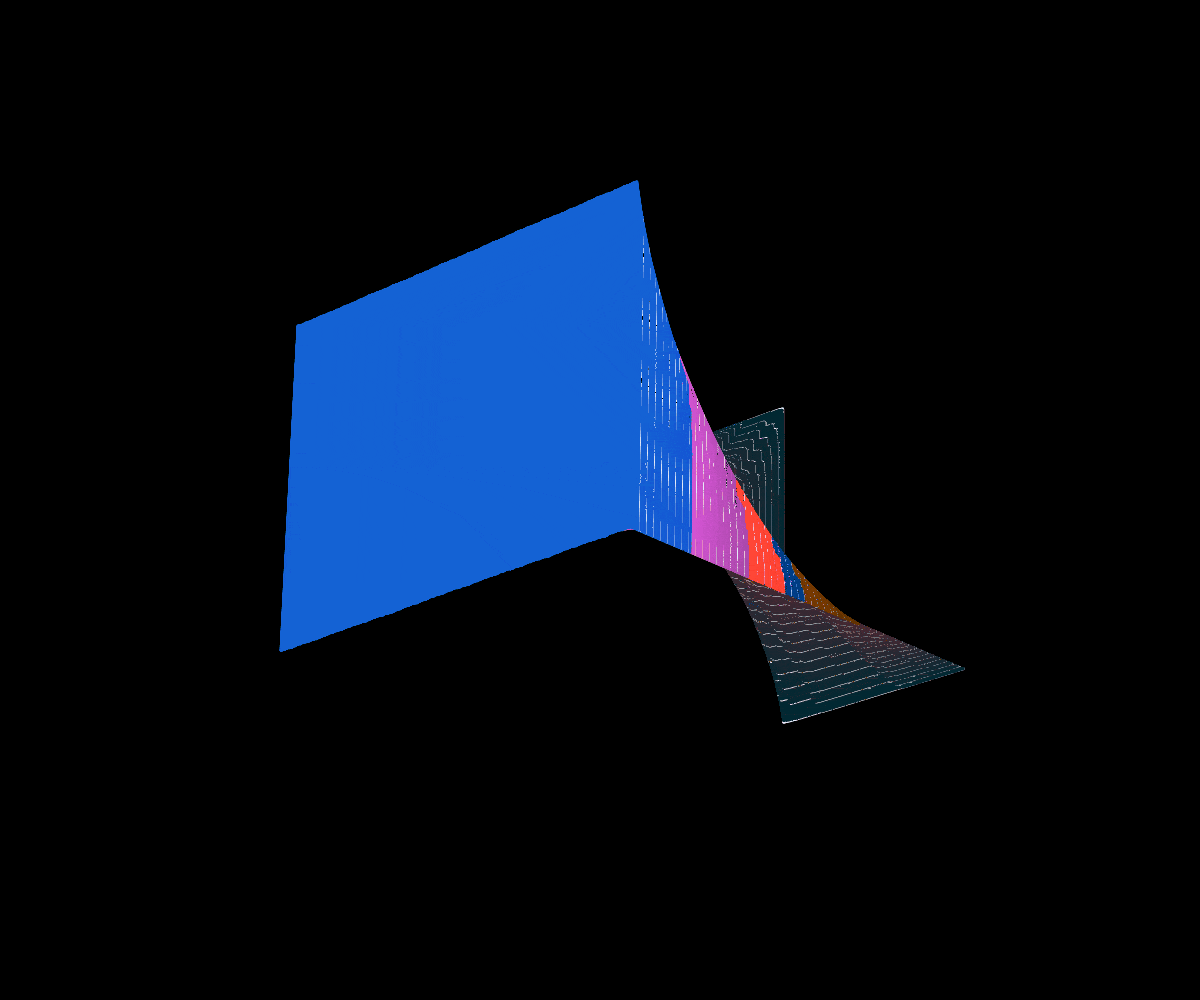
Okamoto’s Function
In 2005, Okamoto introduced a similar family of functions that have a geometrically similar construction to that of Lebesgue’s Singular function.
Interestingly enough, Okamoto’s family of functions captures several different well known fractal graphs as special cases. Namely, the Cantor’s Devil Stair Case function at a=1/2, Bourbaki’s Function at a=2/3, and Perkin’s Function at a=5/6.
*Below a values close to 0 are in green and a values close to 1 and near some important values in blue, the cross-section animation obeys this convention as well.


Cantor's Devil Staircase (a=1/2)
Bourbaki's Function (a=2/3)

Perkin's Function (a=5/6)
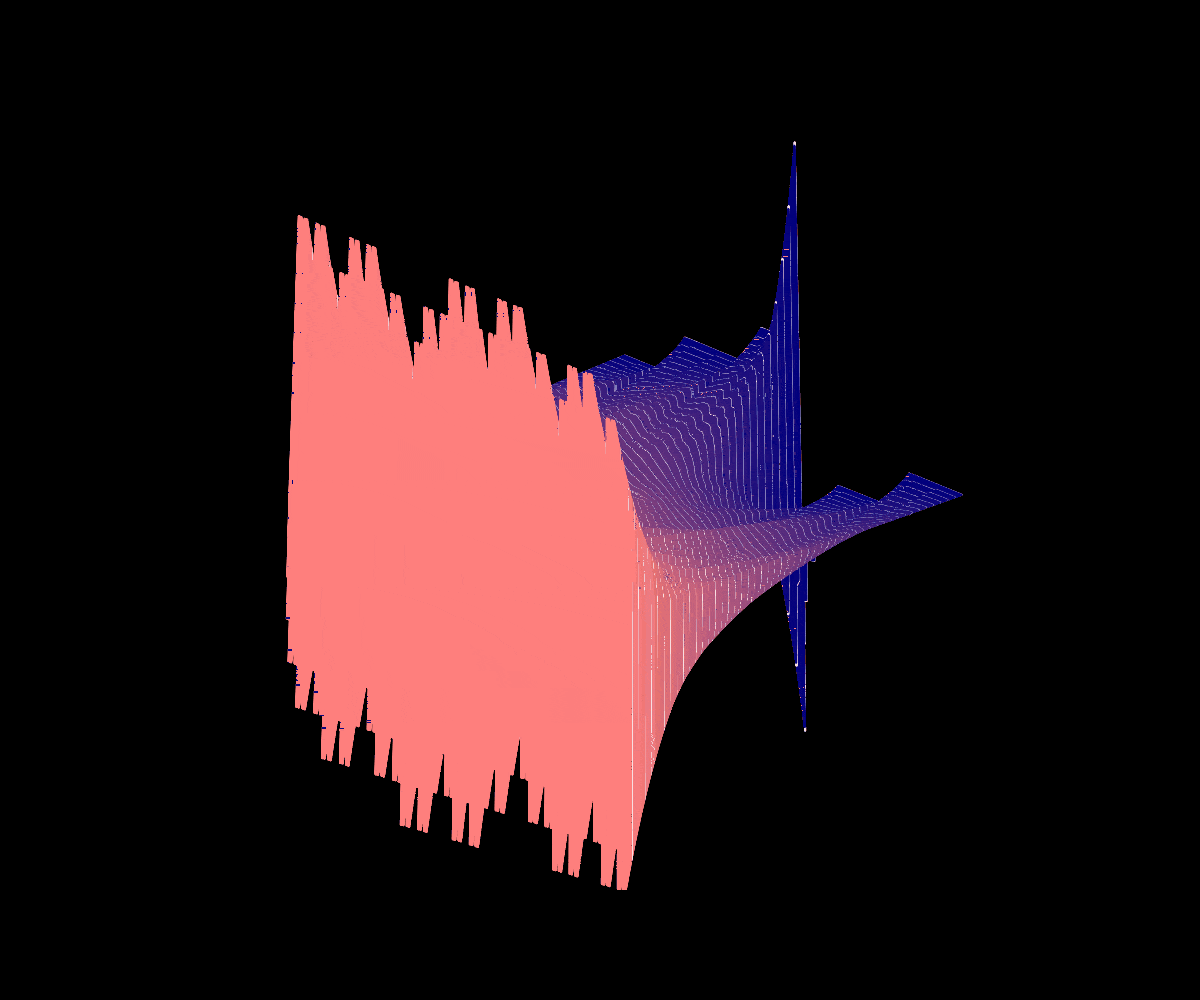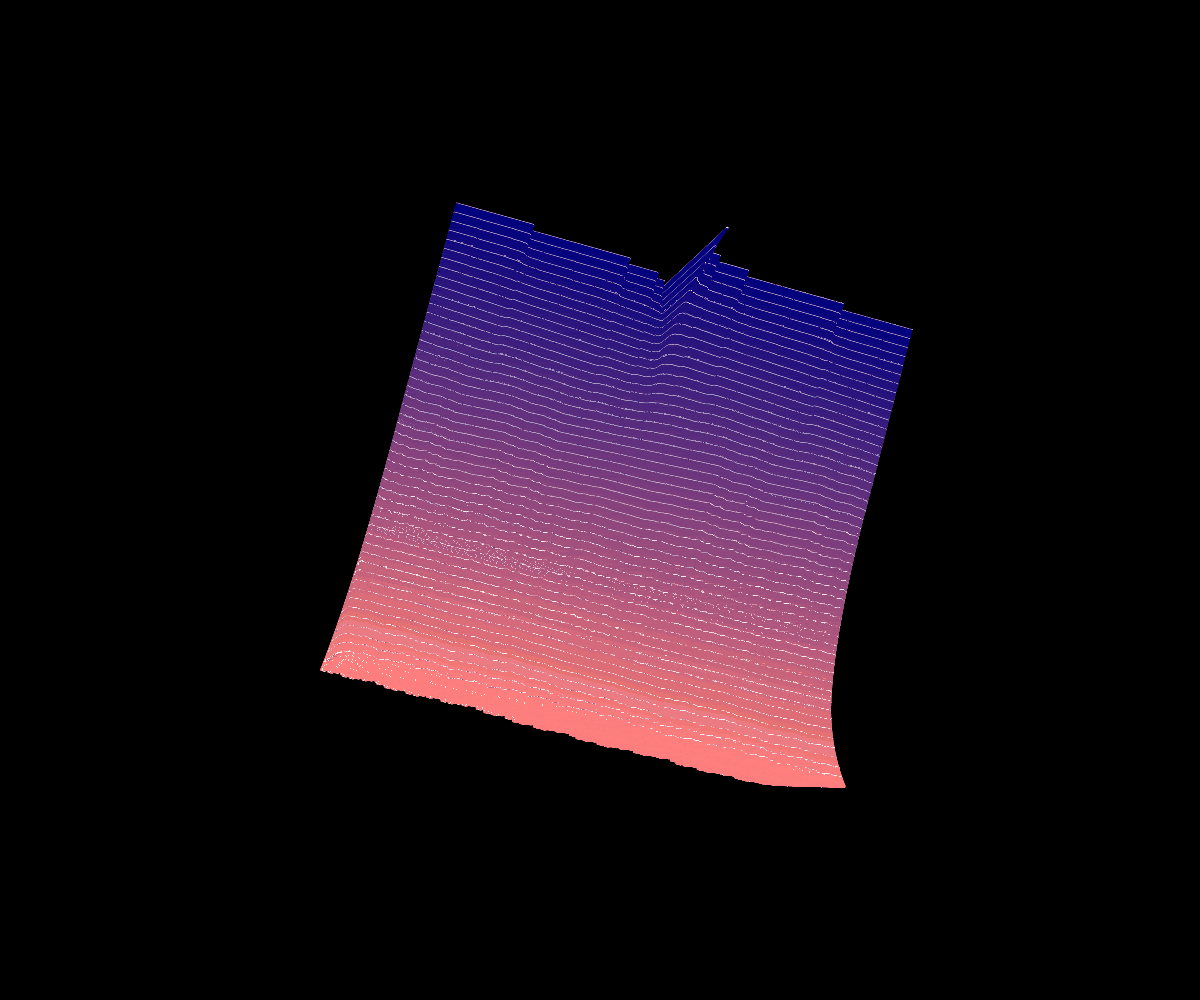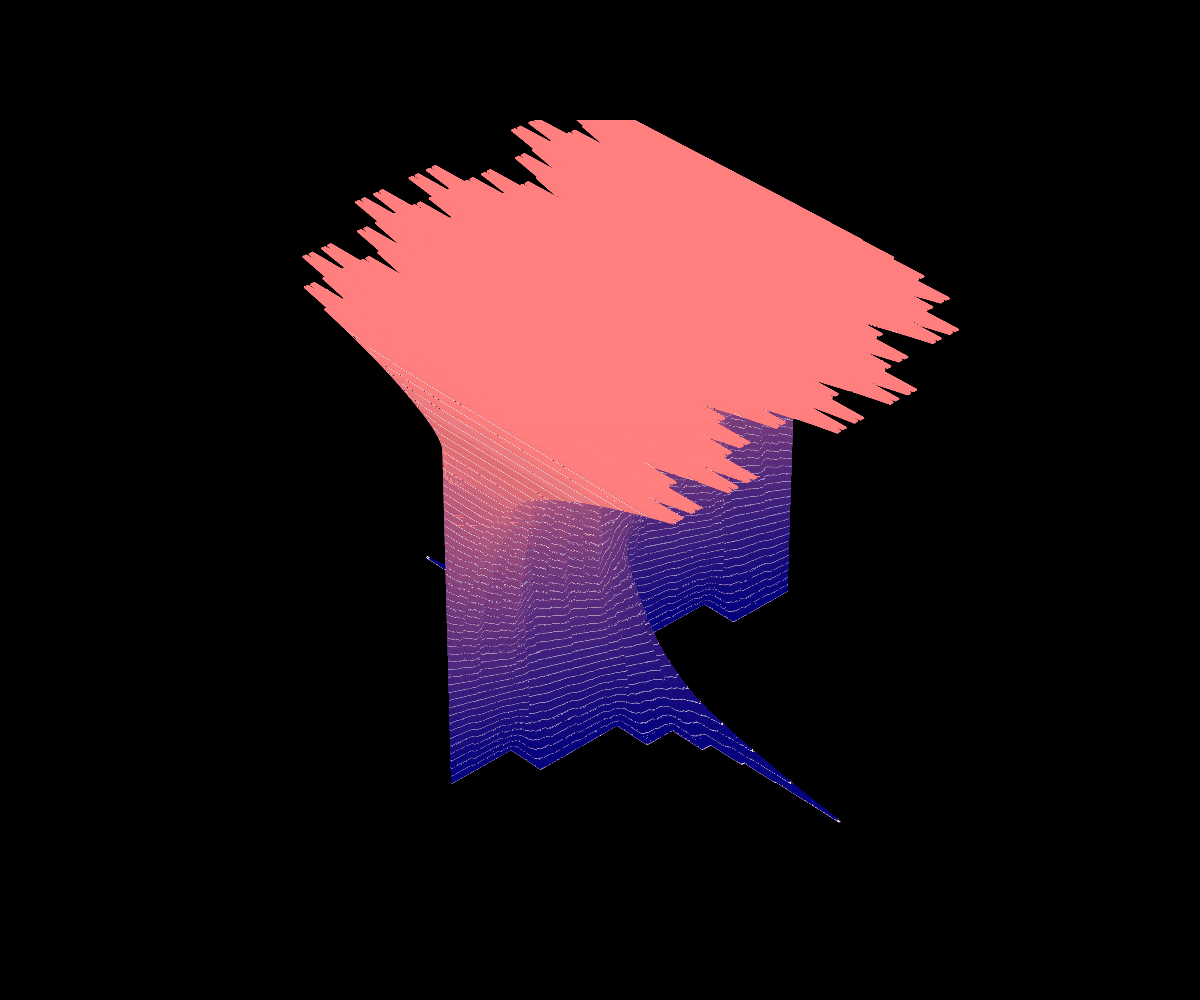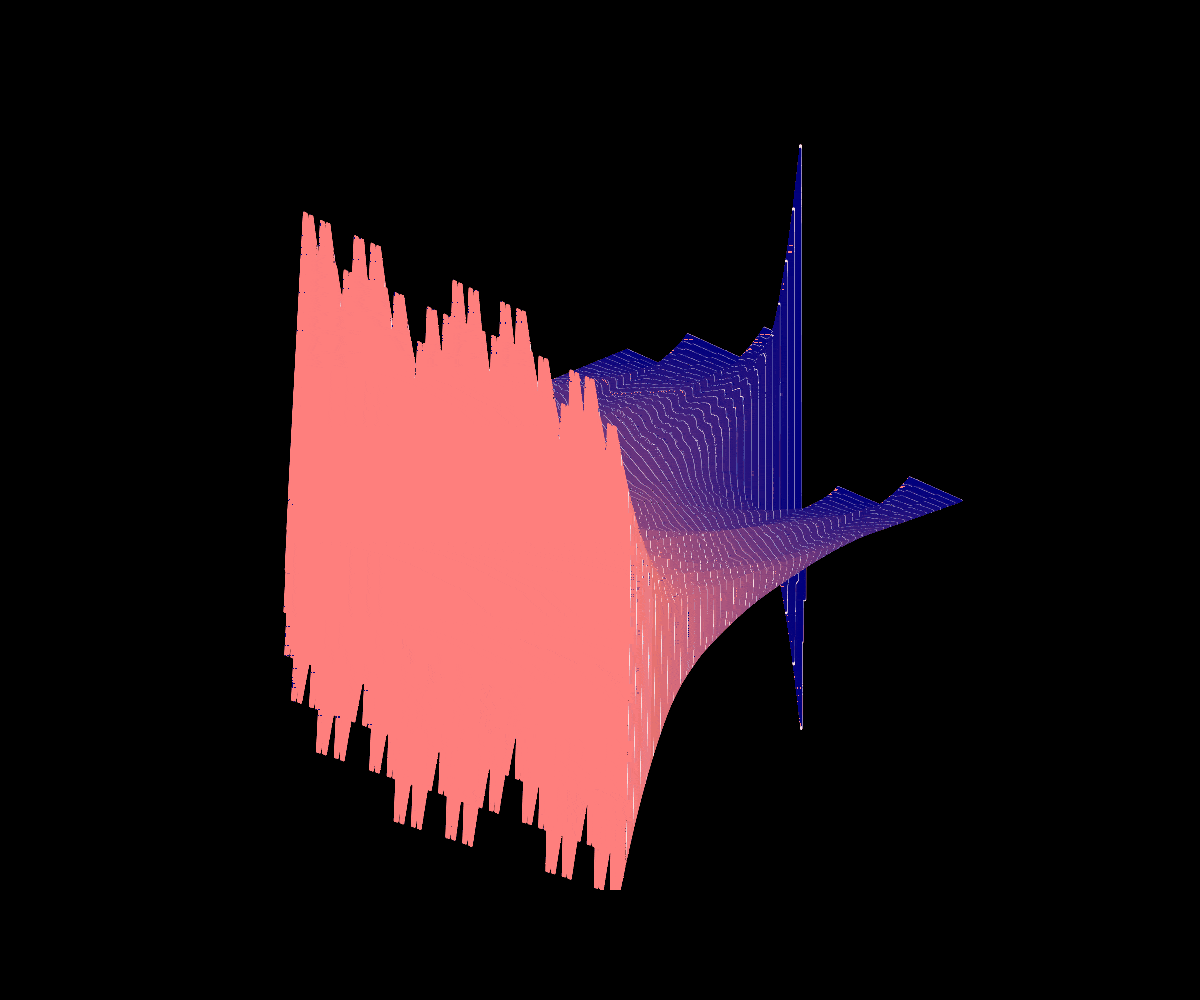
Partial Derivative of Okamoto’s Function
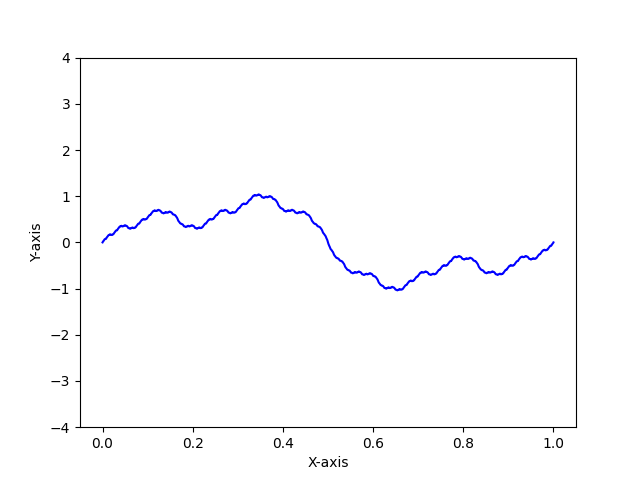
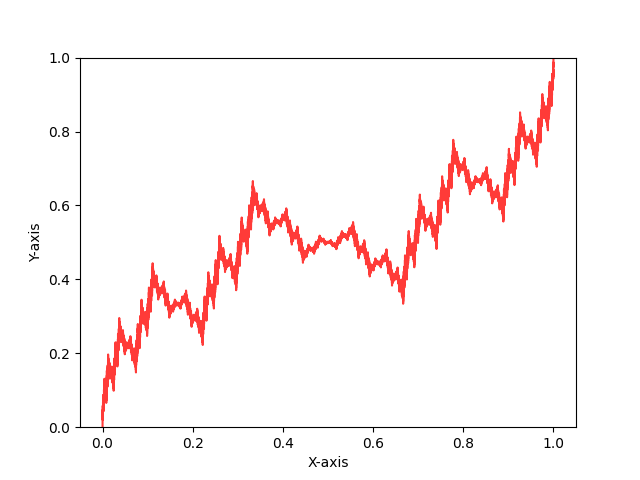
K(x), the partial derivative of Okamoto’s function with respect to the parameter at a=1/3
In 2023, my coauthors and I published a paper analogizing an analysis of the partial derivative of Lebesgue’s singular function at a=1/2 (where the resulting cross-section of the surface is the identity map and the resulting partial with respect to the parameter is a scalar multiple of Takagi’s Function) to the analogous case of a=1/3 for Okamoto’s function.
We were able to completely classify the infinite derivatives of the resulting function K(x) and determine some pathological properties of the set of these points’ Lebesgue measure and Hausdorff dimension. Although it is not covered in our initial paper, we are also interested in looking into the surface of all partial derivatives pictured below.